What is Zero Knowledge Proof In Blockchain & Crypto?

What is Zero Knowledge Proof?

“Zero-knowledge proofs (ZKPs) are cryptographic protocols that enable proving the validity of information without revealing sensitive data.” 

This is the essence of Zero-Knowledge Proofs (ZKPs) – cryptographic methods that allow one party (the prover) to convince another party (the verifier) that a statement is true, without revealing any additional information beyond the truth of the statement itself.

Zooko, the co-founder of Zcash demonstrates Zk proof.

Zooko Wilcox used a simple analogy involving two hidden bits, challenging his partner to prove they were different without revealing their individual values. The process involved Zooko repeatedly swapping or not swapping the hidden bits behind his back, with the assistant correctly identifying the action each time. 

He emphasized that after many repetitions, he became convinced the bits were indeed different, as a bluff (if the bits were identical) would eventually be exposed.  Crucially, even after 100 trials, Zooko gained no information about the actual values of the bits (e.g., whether they were 0 and 1 or 1 and 0), only the single fact that they were different.

Basic Requirements Of Zk Proof Mechanism 

A zk proof must fulfill two basic requirements: completeness and soundness. In Zk proof, completeness means that the prover can show that they know the relevant information with a high degree of probable accuracy.

The verifier must be able to reliably tell whether or not the prover has the information for the proof to be valid. Lastly, for the proof to be truly zero-knowledge, it must be both complete and sound, and the prover and verifier must never share the information in question.

A Short History of Zero-Knowledge Proof
Shafi Goldwasser and Silvio Micali wrote a paper at MIT in 1985 that was the first to talk about the idea of a zero-knowledge proof. They showed that it was possible to show that a number had certain properties without giving away the number or any other information about it. This paper also presented the mathematically significant discovery that interactions between a prover and a verifier can diminish the quantity of information necessary to substantiate a particular theorem.

Nir Bitansky, Ran Canetti, Alessandro Chiesa, and Eran Tromer published Bitansky et al., which was a big step forward. This work was very important in moving the field forward toward Zero-Knowledge Succinct Non-Interactive Arguments of Knowledge (ZK-SNARKs).

Pinocchio made Practical Verifiable Computation possible in 2013.Bryan Parno, Craig Gentry, Jon Howell, and Mariana Raykova, further solidified the practicality of ZK-SNARKs. Pinocchio was a built system for efficiently verifying general computations, offering a concrete implementation that demonstrated efficient verification and compact proof size (only 288 bytes, regardless of computation complexity).

It was one of the first systems to show that verification could be cheaper than native execution for some applications, and it introduced an end-to-end toolchain for compiling C programs into verifiable computations.

Jens Groth’s Groth16 became one of the most popular and well-optimized ZK-SNARK schemes. It worked much better than older designs like Pinocchio, especially for arithmetic circuits. It has helped the development of zk proof a lot, but it needs a trusted setup.

Zcash was created in 2015, and the use of zk proof technology grew.

The “trusted setup” or “Zcash Ceremony” was a very important part of Zcash’s early implementation. The protocol started to make advanced cryptography. The introduction of Zcash brought in multi-party computation to make secure public parameters, which lowered the risk of compromise.

Benedikt Bunz, Jonathan Bootle, Dan Boneh, Andrew Poelstra, Pieter Wuille, and Greg Maxwell came up with “Bulletproofs” in 2017. One of the most important new features of Bulletproofs is that they can make proofs that are logarithmically sized without needing a trusted setup.

This openness makes it much less likely that people will have to make trust assumptions.

Bulletproofs are great for range proofs, which check that a secret number is within a certain range without giving away the number itself. This makes them perfect for private transactions in cryptocurrencies like Monero.

Two Types of ZK Proofs

There are two main types of ZK proofs: interactive and non-interactive. Each type has its own way of securely checking information without giving away private information.

Interactive ZK Proofs

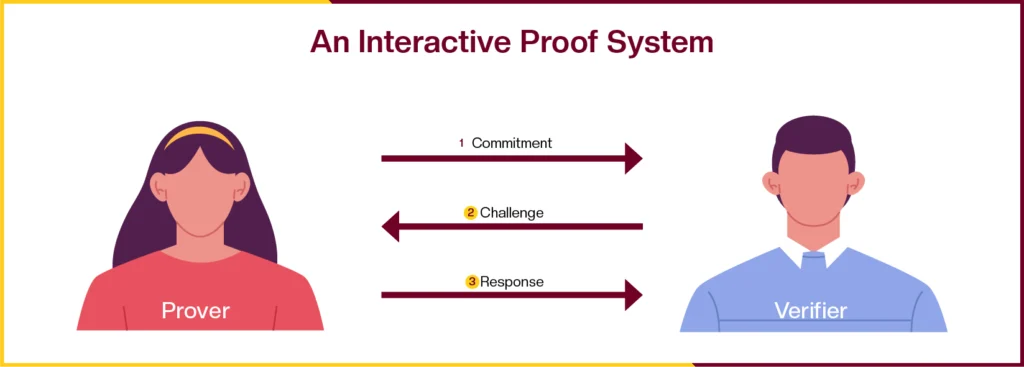
In this type, the person who is proving something and the person who is verifying it talk to each other back and forth to prove that the statement is true. This type of zk proof is ideal for transactions or communication that are more complex and requires both the parties to be involved. This exchange may be repeated multiple times to increase the verifier’s confidence that the prover truly knows the secret.

The biggest advantage of using interactive zk proofs is that you do not need to invest in a trusted set up where each and every user on the network is governed by an administrator. This makes interactive zk-proof a better option for using it in scenarios where global compliance needs to be met.

Non-interactive ZK Proofs

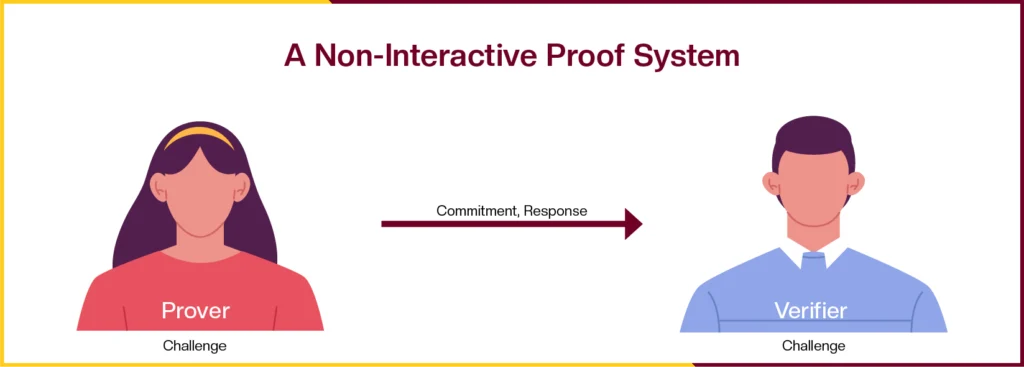
In non-interactive zk proofs the party that wants to get an input validated simply shares the input and if the input is correct the other party says it is accurate/ correct. As the term non-interactive suggests, this type of communication is limited and does not require back and forth communication between both the parties.

Non-interactive proofs eliminate the need for back-and-forth communication between the prover and verifier, offering a streamlined verification process. However, this “simplicity” pertains to the interaction model, not necessarily a reduction in computational complexity. Often, these proofs rely on a trusted setup phase or specific cryptographic assumptions to ensure their security and validity.

Non-Interactive Zero Knowledge Proofs (NIZKPs) are a key part of systems that protect privacy and can be verified in a world that is becoming more digital and decentralized. They let us believe claims without having to trust the source or give away private information.

A trusted setup has been used by many non-interactive ZKPs in the past, especially some ZK-SNARKs like Groth16.

A trusted setup requires a one-time, multi-party computation to create public parameters (called a Common Reference String or CRS) that are very important for the proof system’s security.

The “trusted” part means that it is essential to believe that certain secret random values, called “toxic waste,” were really destroyed during this setup. If any participant kept these secrets, they could make fake proofs that would destroy the system’s integrity.

Even though complicated multi-party ceremonies have tried to reduce this risk by spreading trust, the fact that some level of trust is needed in the beginning has always been a worry.

How Does Zk Proof Technology Work? 

Zero-Knowledge Proofs (ZKPs) use advanced cryptographic tools to let one person (the prover) convince another (the verifier) that a statement is true without giving away any information other than that the statement is true.

Elliptic curve cryptography and polynomial commitments are two types of math that zk proofs use. Let’s look at an example to make this clearer. If you have a hard math problem and want to show that you know the answer without really showing the steps or the answer,

In a ZKP system, a polynomial equation changes the “problem.” After that, the prover makes a polynomial commitment, which is a short, fixed-size way to show the values of a polynomial without giving away the polynomial itself.

You can’t see the answer, but you know it’s there and hasn’t changed. This promise is like sealing a folded piece of paper with the answer inside.

This is like embedding a solution that needs to be solved by the verifier. The missing areas in the equation is where the answer will go. If the person who wants to validate his or her input is indeed sharing the right data then he or she will be able to validate it.

The “zero-knowledge” aspect comes from the fact that the polynomial commitment and the verification process only reveal whether the committed polynomial satisfies the required properties, not the polynomial’s coefficients or the secret witness used to construct it.

This is akin to a magician proving a card is in a specific position in the deck without showing you the card itself or how they knew its position. The “proof” is a short cryptographic string that the verifier can check quickly, regardless of the complexity of the original statement.   

Let’s understand the technical aspect of the elliptical curve with an example.

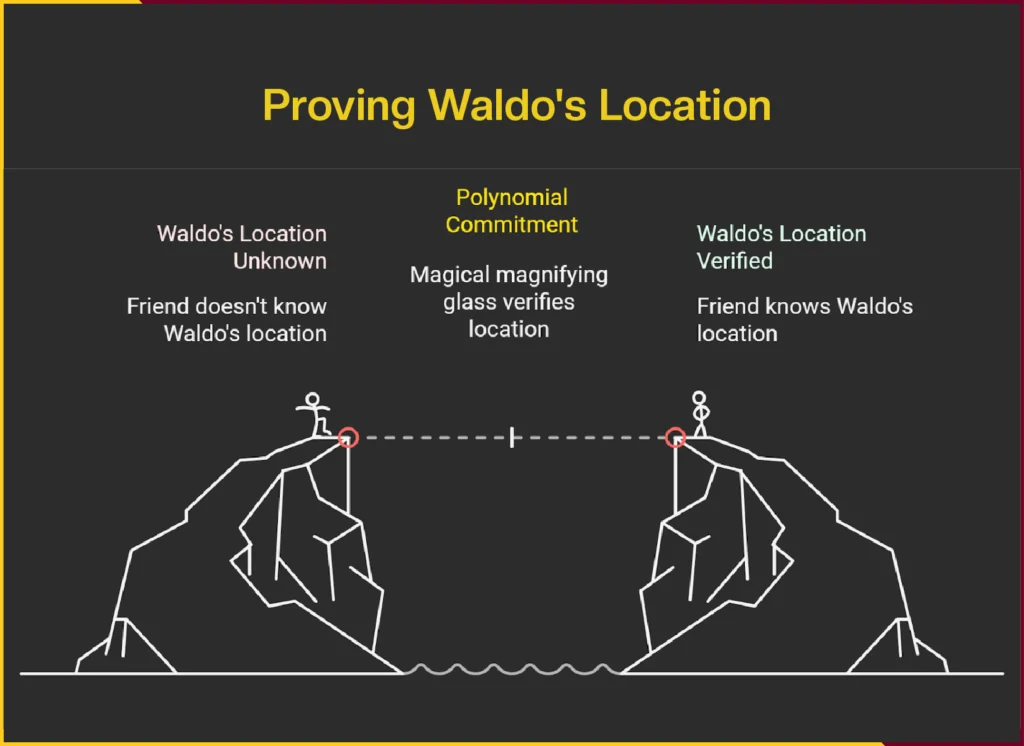
Picture a huge book called “Where’s Waldo?” You found Waldo on a certain page, but you want to show your friend that you did without actually showing them the book or pointing to Waldo.

Why? It could be a game, and you don’t want to ruin their fun by giving them the information they need to find him, or the book might have private information that you don’t want to share.

So, the problem here is to find Waldo. The “solution” or “secret witness” is your knowledge of where Waldo is on the page.

So, how do you prove Waldo’s existence in the book? Using magic. Yes, it sounds out of the world, but it is true. Let’s understand this in detail.

Instead of showing the book, you have a special, opaque, magical magnifying glass. This isn’t just any magnifying glass; it’s designed so that when you place it over the page where you’ve found Waldo, it glows green if Waldo is indeed directly under it, and red if he’s not.

The key is that it only tells you “yes” or “no” it doesn’t show you Waldo, the page, or any other part of the book. This magical magnifying glass is your polynomial commitment. It’s a compact, unrevealing representation of your knowledge.

Now, let the magic begin. In zk-proof elliptical cryptography opens doors for data verification with limited knowledge sharing (to preserve confidentiality).

You let your friend hold the magnifying glass and place it over the exact spot where you claim Waldo is. If it glows green, your friend is convinced you know where Waldo is. They’ve verified your claim without ever seeing Waldo, the page, or the entire book. They’ve only confirmed the truth of your statement (“Waldo is at this spot”).

Applications & Use Cases For Zero Knowledge Proof

Compared to layer 1 blockchains, zero knowledge proof based protocols have a range of benefits that can be beneficial for industries like banking, identity management service providers, healthcare and supply chain management.

In this section, we will explore the various use cases for zero knowledge proof.

Financial Services

Confidentiality in transactions: In crypto, private transactions can be enabled. This function will allow you to hide certain details like sender, recipient, amount etc. This function will allow you to verify the transaction without having to disclose any confidential information. Examples: Zcash, ING Bank’s ZKRP for mortgage applications to prove income within a range without revealing the exact salary.

KYC & AML Verification

Streamlining compliance by allowing individuals to prove they meet KYC/AML requirements (e.g., “I am over 18,” “I am a resident of X country”) without disclosing their full identity documents or sensitive personal data to every service provider.

Identity Management & Authentication

One of the most important applications of zk proof is using it in identifying management systems that allow for seamless and private verification processes. This application makes the whole process of verifying identity secure as users do not have to share all details pertaining to their existence. Simply proving that their identity is valid is enough to pass through the identification system.

Healthcare & Supply Chain Management System

Zk proof allows healthcare providers to validate patient records, insurance eligibility, or medical certifications without exposing sensitive patient information. Researchers can also use zk proof to check aggregated data or specific attributes within datasets without putting individual patient privacy at risk.

There are many ways to use zk proof in the supply chain. Supply chain management can help you find out where a product came from, how it got there, and whether or not it’s real, all without giving away trade secrets or private information about suppliers. This can help stop fake products and make sure that goods are sourced ethically.

In addition, zk proofs can also help in proving adherence to regulations, quality standards, or sustainability practices throughout the supply chain without exposing confidential business information.

Online Voting System

Voting management systems automated with zk proof can enable voter anonymity as it allows voters to cast their ballots and have them verified as legitimate without revealing their identity or vote, ensuring both privacy and election integrity. It enables public verification of election results without compromising individual voter privacy.

Protocols Using Zero-Knowledge Proof

Some of the most popular platforms that use zk proof technology are for example Loopring, Immutable X and Starknet and ZkSync.

Loopring

Loopring is a decentralized exchange (DEX) protocol that uses zk-SNARKs (Zero-Knowledge Succinct Non-Interactive Arguments of Knowledge) to make trading fast and cheap. It does order book management and transaction execution off-chain, which keeps things safe by checking ZKPs on-chain.

Immutable X

It is a layer 2 scaling solution made just for NFTs and blockchain games. Immutable X uses ZKPs to offer instant, gas-free NFT minting and trading. This solves the problems of scalability and cost that have kept NFTs from becoming widely used on Ethereum.

Starknet

Starknet is a decentralized validity rollup (zk-rollup) that uses zk-STARKs (Zero-Knowledge Scalable Transparent Arguments of Knowledge) to achieve massive scalability for any dApp. It is important to note that this infrastructure does not need a trusted set up to function. Starknet executes transactions in bulk and uses STARK proofs to allow the Layer 1 (Ethereum) to verify these transactions with minimal computational effort, emphasizing accuracy and efficiency.

Risks & Challenges in Zero Knowledge Proof 

Following are some of the major challenges prevalent in implementing zk proof technology in day to day life.

For the prover, making ZKPs can take a lot of computer power, especially for big datasets or complicated statements. This takes a lot of time and processing power. Verification usually goes quickly, but making the proof can take a long time.

When you submit ZKPs to a blockchain, you have to pay gas fees. ZK-Rollups, on the other hand, spread these costs out over many transactions, so the cost per transaction is much lower than for direct mainnet transactions.

The ZKP field is changing quickly, which is causing a lot of different protocols, implementations, and cryptographic assumptions to come up. There aren’t any universal rules for how to build, connect, and make ZKPs work with different platforms.

ZKPs make privacy better for users, but they can make regulators worry about compliance with anti-money laundering (AML), know-your-customer (KYC), and counter-financing of terrorism (CFT) rules.

Some people might think that being able to do transactions or prove things without giving away the data behind them makes it easier for criminals to do business.

Wrapping Up

Zero Knowledge Proofs are a super useful and advanced piece of technology used in businesses and organizations for a different array of purposes. Multi party computation can be done in auditing firms by simply setting up a trusted network and updating the blockchain with audits and its related information without having to deal with a third party software.

In contrast to this, zk proofs can also be used in cases where users need to interact with each other in order to validate a transaction. Zk proof tech can be used in CBDCs, speculative crypto investing and identity management systems spanning across the globe. Zk proofs take decentralized blockchain application systems a notch higher.